Решение уравнений содержащих модуль. Раскрытие модуля.

Абсолютная величина числа, или модуль, а вычисляется в соответствии с такими правилами:

Для краткости записи применяют |а|. Так, |10| = 10; -¹/₃= |¹/₃|; | -100| =100 и т. д.

Всякой величине х соответствует достаточно точная величина |х|. И значит тождество у= |х| устанавливает у как некоторую функцию аргумента х.

График этой функции представлен ниже.

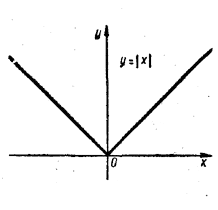
Для x > 0 |x| = x, а для x < 0 |x|= -x; в связи с этим линия у = |x| при x > 0 совмещена с прямой у =х (биссектриса первого координатного угла), а при х < 0 - с прямой у = -х (биссектриса второго координатного угла).

Отдельные уравнения включают в себя неизвестные под знаком модуля.

Произвольные примеры таких уравнений - |х— 1| = 2, |6 — 2х| =3х+ 1 и т. д.

Решение уравнений содержащих неизвестную под знаком модуля базируется на том, что если абсолютная величина неизвестного числа х равняется положительному числу а, то само это число х равняется или а, или -а.

Например:, если |х| = 10, то или х=10, или х = -10.

Рассмотрим решение отдельных уравнений.

Проанализируем решение уравнения |х- 1| = 2.

 Раскроем модуль тогда разность х - 1 может равняться или + 2, или - 2. Если х - 1 = 2, то х = 3; если же х - 1 = - 2, то х = - 1. Делаем подставновку и получаем, что оба эти значения удовлетворяют уравнению.

Ответ. Указанное уравнение имеет два корня: x₁ = 3, x₂ = - 1.

Проанализируем решение уравнения | 6 — 2х| = 3х+ 1.

После раскрытия модуля получаем: или 6 - 2х= 3х+ 1, или 6 - 2х= - (3х+ 1).

В первом случае х = 1, а во втором х= - 7.

Проверка. При х = 1 |6 — 2х| = |4| = 4, 3x + 1 = 4; от суда следует, х = 1 - корень данного уравнения.

При x = - 7 |6 — 2x| = |20| = 20, 3x+ 1= - 20; так как 20 ≠ -20, то х = - 7 не является корнем данного уравнения.

Ответ. У уравнения единственный корень: х = 1.

Уравнения такого типа можно решать и графически.

Так решим, например, графически уравнение |х- 1| = 2.

Первоначально выполним построение графика функции у = |x— 1|. Первым начертим график функции у=х- 1:

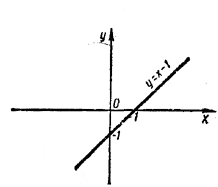
Ту часть этого графика, которая расположена выше оси х менять не будем. Для нее х - 1 > 0 и потому |х-1|=х-1.

Часть графика, которая расположена под осью х, изобразим симметрично относительно этой оси. Поскольку для этой части х - 1 < 0 и соответственно |х - 1|= - (х - 1). Образовавшаяся в результате линия (сплошная линия) и будет графиком функции у = |х—1|.

Эта линия пересечется с прямой у = 2 в двух точках: M₁с абсциссой -1 и М₂ с абсциссой 3. И, соответственно, у уравнения |х- 1| =2 будет два корня: х₁= - 1, х₂= 3.