Тригонометрические функции - это периодические функции с периодами 
для sin, cos, sec и cosec, и 
для tg и ctg.
Зачастую тригонометрические функции обозначают отношением сторон прямоугольного треугольника либо длины конкретных отрезков в единичной окружности.
Прямые тригонометрические функции.
- синус (sin x)
- косинус (cos x)
Производные тригонометрические функции.
- тангенс (tg x)
- котангенс (ctg x)
Другие тригонометрические функции.
- секанс (sec x)
- косеканс (cosec x)
В современном мире есть 6 базовых тригонометрических функций, которые ниже в таблице указаны вместе с уравнениями, которые связывают их.
|
Функция |
Соотношение |
|
sin |
|
|
cos |
|
|
tg или tan |
|
|
ctg или cot |
|
|
sec |
|
|
cosec или csc |
|
Знаки тригонометрических функций .
Значения тригонометрических функций.
Значения sin, cos, tg, ctg, sec и cosec для определенных углов указаны в таблице. («∞» обозначает, что функция в данной точке не определена, а в её окрестности стремится к бесконечности).
|
α |
0° |
30° π/6 |
45° π/4 |
60° π/3 |
90° π/2 |
180° π |
270° 3π/2 |
360° 2π |
|
sinα |
0 |
|
|
|
1 |
0 |
-1 |
0 |
|
cosα |
1 |
|
|
|
0 |
-1 |
0 |
1 |
|
tgα |
0 |
|
1 |
|
|
0 |
|
0 |
|
ctgα |
|
|
1 |
|
0 |
|
0 |
|
|
sec α |
1 |
|
|
2 |
|
-1 |
|
1 |
|
cosec α |
|
2 |
|
|
1 |
|
-1 |
|
Значения тригонометрических функций на окружности.
Таблица значений тригонометрических функций sin , cos , tg для наиболее популярных углов (таблица Брадиса).
|
α(град) |
0 |
15 |
30 |
45 |
60 |
75 |
90 |
|
α(рад) |
0 |
π/12 |
π/6 |
π/4 |
π/3 |
5π/12 |
π/2 |
|
sin |
0 |
0,259 |
0,5 |
0,707 |
0,866 |
0,966 |
1 |
|
cos |
1 |
0,966 |
0,866 |
0,707 |
0,5 |
0,259 |
0 |
|
tg |
0 |
0,268 |
0,577 |
1 |
1,732 |
3,732 |
- |
|
ctg |
- |
3,732 |
1,732 |
1 |
0,577 |
0,268 |
0 |
|
α(град) |
120 |
135 |
150 |
180 |
270 |
360 |
|
α(рад) |
2π/3 |
3π/4 |
5π/6 |
π |
3π/2 |
2π |
|
sin |
0,866 |
0,707 |
0,5 |
0 |
-1 |
0 |
|
cos |
-0,5 |
-0,707 |
-0,866 |
-1 |
0 |
1 |
|
tg |
-1,732 |
-1 |
-0,577 |
0 |
- |
0 |
|
ctg |
-0,577 |
-1 |
-1,732 |
- |
0 |
- |
Свойства тригонометрических функций.
1. Элементарные тождества тригонометрических функций.
2. Непрерывность тригонометрических функций.
sin, cos — непрерывные функции. tg, sec имеют точки разрыва ±90°, ±270°, ±450°, …; ctg, cosec — 0°, ±180°, ±360°, … .
3. Чётность тригонометрических функций.
4. Периодичность тригонометрических функций.
5. Формулы приведения тригонометрических функций.
6. Формулы сложения тригонометрических функций.
7. Формулы для кратных углов тригонометрических функций.
sin 2 α = 2 sin α cos α;
cos 2α = cos2 α – sin2 α = 2 cos2 α – 1 = 1 – 2 sin2 α;
sin 3α = 3 sin α – 4 sin3 α;
cos 3α = 4 cos3 α – 3 cos α;
Когда в формулах двойного аргумента заменяют α на α/2, то легко изменить в формулы половинных углов:
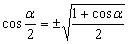
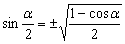
8. Произведения тригонометрических функций.
9. Степени тригонометрических функций:
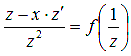
10. Однопараметрическое представление тригонометрических функций.
Каждую тригонометрическую функцию легко выразить через tg половинного угла.
Разбор ЕГЭ 2013 по математике. Задание С1
