Тригонометрические функции. Выражение и преобразование тригонометрических функций формулы.

Тригонометрические тождества — математические выражения для тригонометрических функций, выполняющиеся при всех значениях аргумента (из общей области определения).

Формулы универсальной подстановки.

С этими формулами легко любое выражение, которое содержит различные тригонометрические функции одного аргумента, превращается в рациональное выражение одной функции tg (α /2):

Формулы преобразования сумм в произведения и произведений в суммы.

Раньше приведенные формулы использовали для упрощения расчетов. Вычисляли при помощи логарифмических таблиц, а позднее – логарифмической линейки, так как логарифмы наилучше подходят для умножения чисел. Вот почему каждое исходное выражение приводилось к виду, который был бы удобен для логарифмирования, то есть к произведениям, например:

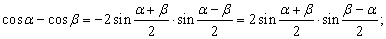
2 sin α sin b = cos (α – b) – cos (α + b);

2 cos α cos b = cos (α – b) + cos (α + b);

2 sin α cos b = sin (α – b) + sin (α + b).         

где  - угол, для которого  в частности,

Формулы для функций тангенса и котангенса легко получаются из выше указанных.

Формулы понижения степени.

При помощи данных формул тригонометрические уравнения легко приводятся к уравнениям с более низкими степенями. Точно так же выводят формулы понижения для более высоких степеней sin и cos.

Выражение тригонометрических функций через одну из них того же аргумента.

Знак перед корнем зависим от четверти расположения угола α.

Через sinα:

Через cosα:

Через tgα:

Через ctgα:

Универсальная подстановка через тангенс половинного аргумента.

Рассчитать тригонометрические и другие формулы вы можете на нашем инженерном калькуляторе онлайн.