Числа. Модуль и аргумент комплексного числа.

Модуль комплексного числа.

Число r — длина радиус-вектора точки M (x, y)является модулем комплексного числа z = x + iy. Обозначается как .

Из рисунка получаем формулу для определения модуля числа, которое задано в алгебраической форме z = x + iy:

Видно, что  и  лишь для числа .

При помощи правила вычитания записываем модуль числа z = z₁ – z₂, где z₁ = x₁ + iy₁ и z₂ = x₂ + iy₂:

А это является формулой для расстояния между точками  и .

Т.о., число  - это расстояние между точками z₁ и z₂ на комплексной плоскости.

Пример. Найдем модули комплексных чисел:

Рассчитаем решение для всех 3-х случаев:

1) z₁ и z₂ являются числами действительными, при этом . Значит, ;

2) числа  и  являются чисто мнимыми, при этом . Значит, , т.е. , либо ;

3) для числа  имеем . Поэтому .

Аргумент комплексного числа.

Полярный угол φ точки M (x, y) является аргументом комплексного числа z = x + iy. Обозначается как .

Формулу для определения аргумента комплексного числа z = x + iy, который задан в алгебраической форме, получаем, пользуясь связью декартовых и полярных координат точки M (x, y).

Для точек, которые не лежат на мнимой оси, то есть для z, у которых , получаем ; для точек мнимой положительной полуоси, то есть для z, у которых , получаем ; для точек мнимой отрицательной полуоси, то есть для z, у которых , получаем .

Аргумент числа  является величиной неопределенной.

Определение аргумента при  сводится к решению тригонометрического уравнения . При , то есть когда  является числом действительным, у нас есть  при  и  при .

При  решение уравнения зависимо от четверти плоскости . Четверть, в которое расположена точка z, определяют по знакам  и . В итоге имеем:

При решении примеров удобно пользоваться схемой:

Пример. Найти аргументы чисел:

.

Решим задачу для каждого из 3-х случаев:

1) числа  и  — действительные, причем , поэтому ;

2) числа  и  — чисто мнимые , причем  , поэтому  ;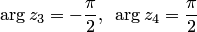

3) для числа  имеем , поэтому из  находим ; так как при этом (точка  находится во второй четверти, то получаем  или .

Пример. Найти модуль и аргумент числа .

Находим . Т.к. , то есть точка расположена в 4 четверти, то из равенства  получаем .