Свойства корней.

Свойства квадратных корней.

• ;

•  если а ≥ 0 и b > 0;

•  если а ≥ 0 и n — натуральное число;

•  если а ≥ 0 и n — натуральное число.

• Обратите внимание, (−5)² = 25, но .

• Корень не может равняться неположительному числу.

•  — невозможно вычислить, корень из отрицательного числа не существует.

• Если , то b² = a, при а ≥ 0 и b ≥ 0, это одно из важнейших свойств корней.

• Важно понимать, что квадратный корень - это другая запись степени ½:

Например:

• Величина корня не изменится, если его показатель увеличить в n раз и одновременно возвести подкоренное значение в степень n:

•   Величина корня не изменится, если показатель степени уменьшить в n раз и одновременно извлечь корень n-й степени из подкоренного значения:

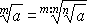
•  Корень от частного равен частному от деления корня из делимого на корень из делителя (показатели корней должны быть одинаковыми):

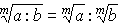
  Обратно:

•   Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное значение:

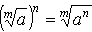
  Обратно, чтобы извлечь корень из степени, достаточно возвести в эту степень корень из основания степени:

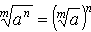
•   Корень из произведения нескольких сомножителей равен произведению корней той же степени из этих сомножителей (тоже важное свойство корней):

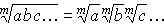
  Обратно, произведение корней одной и той же степени равно корню той же степени из произведения подкоренных значений:

Квадратный корень как элементарная функция.

Квадратный корень – это элементарная функция и частный случай степенной функции  при . Арифметический квадратный корень является гладким при , а в нуле он непрерывен справа, но не дифференцируется (отличительное свойтво корней).

Как функция комплексный переменный корень — двузначная функция, у которой листы сходятся в нуле.

Свойство корня как функции.

На [0; +∞) можно поставить каждому числу х в соответствие единственное число корень n-степени из x при любом значении n.

То есть это означает, что на множестве [0; +∞) можно говорить о функции корня:

Теперь определим свойства функции корня и построим ее график.

Основные свойства корня как функции:

Промежуток [0; +∞) – является областью определения.

Так как неотрицательное число является корнем n-степени из неотрицательного числа, значит промежуток [0; +∞) будет областью значения функции.

Поскольку симметричным множеством не является область определения функции, поэтому данная функция не является ни нечетной, ни четной.

Операция по извлечению корня вводилась как обратная операция возведения в соответствующую степень.

Значит можно утверждать, что:

Теперь можно построить график функции корня.

Пользуясь графиком, можно записать оставшиеся свойства функции.

На промежутке [0; +∞) функция возрастает.

Сверху функция не ограничена, но она ограничена снизу, например, прямой у, которая = -0,5.

На всей области определения функция выпукла вверх.

У функции наименьшим значением будет являться 0, а наибольшего значения она не имеет.

Если в каждой из точек некоторого промежутка функция дифференцируема, то это значит, что на данном промежутке она непрерывна.

Тогда:

В любой точке промежутка [0; +∞) существует эта производная, исключением является только точка 0.

Поскольку в любой точке промежутка (0; +∞) функция имеет производную, значит на промежутке (0; +∞) функция дифференцируема.