Функции корня.

Корнем n-степени из неотрицательного числа a является такое неотрицательное число, при возведении в n-степень которого получается число a.

Корнем нечетной n-степени из отрицательного числа a называется такое отрицательное число, при возведении в n-степень которого получается число a.

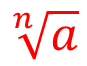
Где n – это показатель корня и a – подкоренное число.

Таким образом, извлечь корень любой степени (от второй и далее) можно из любого неотрицательного числа, а из отрицательного числа извлекается только корень нечетной степени.

На [0; +∞) можно поставить каждому числу х в соответствие единственное число корень n-степени из x при любом значении n.

То есть это означает, что на множестве [0; +∞) можно говорить о функции корня:

Теперь определим свойства данной функции и построим ее график.

Основные свойства функции:

Промежуток [0; +∞) – является областью определения.

Так как неотрицательное число является корнем n-степени из неотрицательного числа, значит промежуток [0; +∞) будет областью значения функции.

Поскольку симметричным множеством не является область определения функции, поэтому данная функция не является ни нечетной, ни четной.

Операция по извлечению корня вводилась как обратная операция возведения в соответствующую степень.

Значит можно утверждать, что:

Теперь можно построить график функции корня.

Пользуясь графиком, можно записать оставшиеся свойства функции.

На промежутке [0; +∞) функция возрастает.

Сверху функция не ограничена, но она ограничена снизу, например, прямой у, которая = -0,5.

На всей области определения функция выпукла вверх.

У функции наименьшим значением будет являться 0, а наибольшего значения она не имеет.

Если в каждой из точек некоторого промежутка функция дифференцируема, то это значит, что на данном промежутке она непрерывна.

Тогда:

В любой точке промежутка [0; +∞) существует эта производная, исключением является только точка 0. Поскольку в любой точке промежутка (0; +∞) функция имеет производную, значит на промежутке (0; +∞) функция дифференцируема.

Рассмотрим несколько примеров графиков функции корня.

Эти примеры касаются функции, у которой у равно корень n-степени из x, только при неотрицательных значениях аргумента.

Но если n является нечетным числом, то для отрицательных х также имеет смысл выражение корень n-степени из x. А значит, говорить можно о функции:

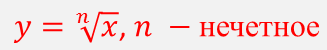
Запишем свойства данной функции.

Промежуток (– ∞; + ∞) является областью определения функции.

Промежуток (– ∞; + ∞) будет областью значений.

Область определения функции является симметричным множеством, значит данную функцию можно исследовать на четность:

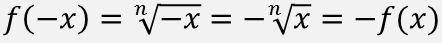
Таким образом получаем, что функция будет нечетной при нечетном n.

Построим график функции.

Добавим к этой ветви еще ветвь, которая симметрична ей относительно начала координат, для этого воспользуемся свойством нечетности функции корня.

• Получившийся график позволяет легко записать оставшиеся свойства функции.
• На всей области определения функция возрастает.
• Ни сверху, ни снизу функция не ограничена.
• У функции нет наибольшего и наименьшего значения.
• На всей области определения функция непрерывна.
• На промежутке (– ∞; 0) функция выпукла вниз, а на промежутке (0; + ∞) она выпукла вверх.
• На всей области определения функция дифференцируема, за исключением точки 0.

Еще несколько примеров графиков функции корня.