Решение простейших дифференциальных уравнений первого порядка.

Простейшие дифференциальные уравнения первого порядка или уже решены относительно производной , или их можно решить относительно производной .

Общее решение дифференциальных уравнений типа  на интервале X, который задан, можно найти, взяв интеграл обоих частей этого равенства.

Получим .

Если посмотреть на свойства неопределенного интеграла, то найдем искомое общее решение:

y = F(x) + C,

где F(x) – одна из первообразных функции f(x) на промежутке X, а С – произвольная постоянная.

Обратите внимание, что в большинстве задач интервал X не указывают. Это значит, что решение нужно находить для всех x, при которых и искомая функция y, и исходное уравнение имеют смысл.

Если нужно вычислить частное решение дифференциального уравнения , которое удовлетворяет начальному условию y(x₀) = y₀, то после вычисления общего интеграла y = F(x) + C, еще необходимо определить значение постоянной C = C₀, используя начальное условие. Т.е., константу C = C₀ определяют из уравнения F(x₀) + C = y₀, и искомое частное решение дифференциального уравнения примет вид:

y = F(x) + C₀.

Рассмотрим пример:

Найдем общее решение дифференциального уравнения , проверим правильность результата. Найдем частное решение этого уравнения, которое удовлетворяло бы начальному условию .

Решение:

После того, как мы проинтегрировали заданное дифференциальное уравнение, получаем:

.

Возьмем этот интеграл методом интегрирования по частям:

Т.о.,  является общим решением дифференциального уравнения.

Чтобы убедиться в правильности результата, сделаем проверку. Для этого подставляем решение, которое мы нашли, в заданное уравнение:

.

То есть, при  исходное уравнение превращается в тождество:

,

поэтому общее решение дифференциального уравнения определили верно.

Решение, которое мы нашли, является общим решением дифференциального уравнения для каждого действительного значения аргумента x.

Осталось вычислить частное решение ОДУ, которое удовлетворяло бы начальному условию . Другими словами, необходимо вычислить значение константы С, при котором будет верно равенство:

.

Значит:

.

Тогда, подставляя С = 2 в общее решение ОДУ, получаем частное решение дифференциального уравнения, которое удовлетворяет первоначальному условию:

.

Обыкновенное дифференциальное уравнение  можно решить относительно производной, разделив 2 части равенства на f(x). Это преобразование будет равнозначным, если f(x) не превращается в нуль ни при каких x из интервала интегрирования дифференциального уравнения X.

Вероятны ситуации, когда при некоторых значениях аргумента x ∈ X функции f(x) и g(x) одновременно превращаются в нуль. Для подобных значений x общим решением дифференциального уравнения  будет всякая функция y, которая определена в них, т.к. .

Если для некоторых значений аргумента x ∈ X выполняется условие , значит, в этом случае у ОДУ  решений нет.

Для всех других x из интервала X общее решение дифференциального уравнения определяется из преобразованного уравнения .

Разберем на примерах:

Пример 1.

Найдем общее решение ОДУ: .

Решение.

Из свойств основных элементарных функций ясно, что функция натурального логарифма определена для неотрицательных значений аргумента, поэтому областью определения выражения ln(x+3) есть интервал x > -3. Значит, заданное дифференциальное уравнение имеет смысл для x > -3. При этих значениях аргумента выражение x + 3 не обращается в нуль, поэтому можно решить ОДУ относительно производной, разделив 2 части на х + 3.

Получаем .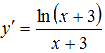

Далее проинтегрируем полученное дифференциальное уравнение, решенное относительно производной: . Для взятия этого интеграла пользуемся методом подведения под знак дифференциала:

.

Т.о.,  - общее решение дифференциального уравнения при x > -3.

Пример 2.

Найдем все решения дифференциального уравнения .

Решение.

Дифференциальное уравнение имеет смысл для всех действительных x. Если принять x ≠ 0, то можно преобразовать ОДУ к виду . При x = 0 начальное уравнение превращается в тождество  для всех функций , которые определены при x = 0.

Значит, при x = 0 решением дифференциального уравнения будет всякая функция y, которая определена при аргументе, равном нулю.

Интегрируем дифференциальное уравнение :

.

Ответ:

 - решение дифференциального уравнения, при x = 0 решением дифференциального уравнения будет всякая функция, которая определена при таком значении аргумента.