Дифференциальные уравнения с разделяющимися переменными.

Дифференциальные уравнения с разделяющимися переменными вида  либо .

Дифференциальные уравнения  являются уравнениями с разделенными переменными.

Название этих дифференциальных уравнений имеет некоторый смысл: выражения, которые содержат переменные x и y, разделены знаком равенства, т.е., находятся по разные стороны от него.

Общее решение дифференциальных уравнений с разделенными переменными можно найти, проинтегрировав обе части равенства: ∫ f(y)dy = ∫ f(x)dx.

В качестве примеров ОДУ с разделенными переменными приведем .

Дифференциальные уравнения с разделяющимися переменными приводят к виду ОДУ (обыкновенных дифференциальных уравнений) с разделенными переменными делением обеих частей уравнения на выражение f₂(y) ⋅ g₁(x).

Т.е., получим:

.

Это преобразование будет равноценным, при f₂(y) ≠ 0 и g₁(x) ≠ 0. В противном случае можно потерять некоторые решения.

Примерами ОДУ с разделяющимися переменными есть:

.

Некоторые дифференциальные уравнения можно свести к уравнениям с разделяющимися переменными при помощи замены переменных.

Дифференциальные уравнения  приводят к ОДУ с разделяющимися переменными подстановкой z = ax+by.

Например, уравнение  при помощи подстановки z = 2x+3y превращается в:

.

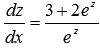ОДУ  либо  видоизменяются к уравнениям с разделяющимися переменными при помощи замен  либо .

К примеру, дифференциальное уравнение  после замены  выглядит так:

.

Некоторые дифференциальные уравнения нужно слегка изменить для того, чтобы можно было сделать замену. Например, можно только поделить на x² либо y² числитель и знаменатель правой части дифференциального уравнения , чтобы оно стало соответствовать  либо  соответственно.

ДУ (дифференциальные уравнения)  видоизменяются к только что рассмотренным ОДУ  либо , если ввести новые переменные:

, где  - решение системы линейных уравнений  

и провести некоторые преобразования.

К примеру, ДУ  после того, как ввели новые переменные  принимает вид:

.

Делим на u числителя и знаменателя правой части уравнения, которое мы получили, и принимаем . В итоге получаем уравнение с разделяющимися переменными .

Дифференциальные уравнения с разделяющимися переменными делятся на:

• Дифференциальные уравнения с разделенными переменными .

• Дифференциальные уравнения с разделяющимися переменными .

• Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными , a ≠ 0, b ≠ 0.

• Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными  или .

• Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными .