Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными.

Дифференциальные уравнения, которые сводятся к уравнениям с разделяющимися переменными делятся на три типа:

• Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными , a ≠ 0, b ≠ 0.
• Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными  или .
• Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными .

Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными , a ≠ 0, b ≠ 0 .

ОДУ 1-го порядка типа , a ≠ 0, b ≠ 0 приводят к уравнениям с разделяющимися переменными введением новой переменной z = ax + by, где z является функцией аргумента x.

В таком случае:

После того, как подставили в начальное уравнение и после некоторых преобразований получаем уравнение с разделенными переменными:

Пример.

Найдем общее решение дифференциального уравнения 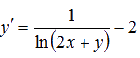 и частное решение, которое удовлетворяло бы начальному условию y(0) = e.

Решение.

Пусть z = 2x + y, значит:

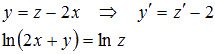
Подставляем результаты, которые мы получили, в начальное уравнение и преобразуем его к ДУ с разделяющимися переменными:

Разделяем переменные и интегрируем две части равенства:

.

Интеграл в левой части находим способом интегрирования по частям, а интеграл в правой части является табличной величиной:

Тогда, .

Примем C = C₂ - C₁ и сделаем обратную замену z = 2x + y, то получаем общее решение дифференциального уравнения в виде неявно заданной функции:

.

Теперь нам нужно найти частное решение, которое удовлетворяло бы исходному условию y(0) = e. Для этого нужно подставить x = 0 и y(0) = e в общее решение дифференциального уравнения и найти значение константы С:

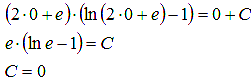
Тогда, частное решение, которое мы ищем, удовлетворяющее условию y(0) = e, имеет вид:

.

Замечание.

В условии задачи не говорится об интервале для нахождения общее решение дифференциального уравнения. В подобных случаях решают пример для всех значений аргумента x, при которых исходное дифференциальное уравнение и его решения имеют смысл. Для нашего примера дифференциальное уравнение имеет смысл при .

Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными   или .

Дифференциальные уравнения типа  либо 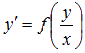 можно свести к ОДУ с разделяющимися переменными, произведя замену  либо , где z – функция аргумента x.

Если , то  и из правила дифференцирования дроби . В этом случае уравнения принимают вид либо .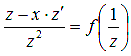

Примем , то y = x ⋅ z и из правила производной произведения . В таком случае уравнения сводятся к  либо .

Рассмотрим на примере:

Решить дифференциальное уравнение .

Решение.

Принимаем , отсюда . Подставляем в исходное уравнение:

Интегрируем полученное уравнение с разделенными переменными:

После обратной замены получаем общее решение исходного дифференциального уравнения в виде неявно заданной функции .

Также рассмотрим дифференциальные уравнения типа:

.

Приводим эти дифференциальные уравнения приводятся к виду  либо 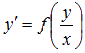 , разделив числитель и знаменатель правой части на yⁿ либо xⁿ.

Например:

Найдем общее решение дифференциального уравнения .

Решение.

В этом примере x и y не равны нулю. Делим и числитель и знаменатель правой части равенства на x²:

Вводим новую переменную , отсюда: .

Подставляем в начальное уравнение:

После подстановки образовалось дифференциальное уравнение с разделенными переменными. Решим это уравнение:

В данном примере можно получить решение и в явном виде.

Для этого принимаем  и пользуемся свойствами логарифма:

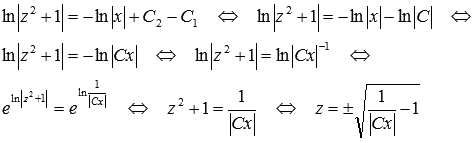
Теперь делаем обратную замену y = x ⋅ z и записываем ответ:

.

Замечание: это уравнение (как и остальные подобного типа) еще решают используя замену .

Опишем решение для такой замены.

Делим числитель и знаменатель на y²:

Пусть , отсюда .

Подставляя все в начальное уравнение, получаем дифференциальное уравнение с разделяющимися переменными:

.

Разделив переменные, получаем равенство . Проинтегрируем его .

Для начала берем интеграл . После разложения на простейшие дроби подынтегральной функции интеграл принимаем вид . Далее интегрируем простейшие дроби:

Находим интеграл :

.

Теперь имеем  либо , где .

После проведения обратной замены  и некоторых преобразований получаем тот ответ: .

Вывод. В нашем примере при замене  решение оказалось более сложным, чем при замене . Выбирайте решение через ту переменную, которая делаем его проще.

Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными .

Дифференциальные уравнения  сводятся к уравнениям либо , значит, к уравнениям с разделяющимися переменными. Для этого находят (x₀ , y₀) - решение системы 2-х линейных однородных уравнений  и вводят новые переменные . После этой замены уравнение примет вид:

.

Разберем на примере.

Пример решения дифференциальных уравнений, сводящихся к уравнениям с разделяющимися переменными.

Найдем общее решение дифференциального уравнения .

Решение.

Составляем и решаем систему линейных уравнений:

Заменяем переменные:

После подстановки в заданное уравнение получили:

.

После деления на u числителя и знаменателя правой части получаем:

.

Вводим новую переменную , тогда:

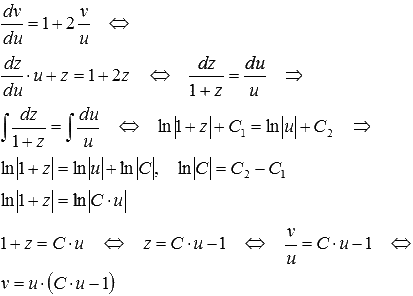
Возвращаемся к исходным переменным, делая обратную замену :

Это есть общее решение дифференциального уравнения.