Простейшие дифференциальные уравнения первого порядка вида 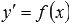 .
.
Приведем несколько примеров подобных дифференциальных уравнений:
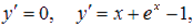
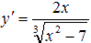 .
.
Дифференциальные уравнения 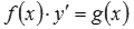 можно решить относительно производной, разделив обе части равенства на f(x). Тогда мы придем к уравнению
можно решить относительно производной, разделив обе части равенства на f(x). Тогда мы придем к уравнению 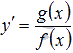 , которое будет соответствовать исходному при f(x)≠ 0.
, которое будет соответствовать исходному при f(x)≠ 0.
Примеры подобных уравнений: 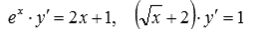 .
.
Если есть значения аргумента x, при которых функции f(x) и g(x) одновременно превращаются в нуль, тогда возникают еще некоторые решения. Дополнительными решениями уравнения  при данных x будут все функции, которые определены для этих значений аргумента.
при данных x будут все функции, которые определены для этих значений аргумента.
Как пример подобных дифференциальных уравнений:
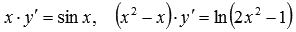 .
.
Решение простейших дифференциальных уравнений первого порядка.
|
|
Калькуляторы по алгебре
|
|
Решения, подсказки и учебник линейной алгебры онлайн (все калькуляторы по алгебре).
|
|
Калькуляторы по алгебре
|
|
|
|
|
Математические калькуляторы
|
|
Математические калькуляторы: корни, дроби, степени, уравнения, фигуры, системы счисления и другие калькуляторы.
|
|
Математические калькуляторы
|
|
|
|
|
|
Решение дифференциальных уравнений
|
|
Дифференциальные уравнения: Бернулли, первого, второго порядка и высшых порядков, с разделенными и разделяющимися переменными, системы ДУ
|
|
Решение дифференциальных уравнений
|
|
|
|
|
Алгебра 6,7,8,9,10,11 класс, ЕГЭ, ГИА
|
|
Основная информация по курсу алгебры для обучения и подготовки в экзаменам, ГВЭ, ЕГЭ, ОГЭ, ГИА
|
|
Алгебра 6,7,8,9,10,11 класс, ЕГЭ, ГИА
|
|
|
|
|
|
|
|
|
Дифференциальные уравнения с разделяющимися переменными.
|
|
Название этих дифференциальных уравнений имеет некоторый смысл: выражения, которые содержат переменные x и y, разделены знаком равенства, т.е., находятся по разные стороны от него.
|
|
Дифференциальные уравнения с разделяющимися переменными.
|
|
|
|
|
|
|
|
|
|
|
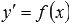 .
.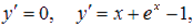
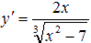 .
.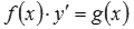 можно решить относительно производной, разделив обе части равенства на f(x). Тогда мы придем к уравнению
можно решить относительно производной, разделив обе части равенства на f(x). Тогда мы придем к уравнению 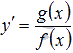 , которое будет соответствовать исходному при f(x)≠ 0.
, которое будет соответствовать исходному при f(x)≠ 0.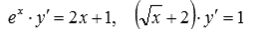 .
. при данных x будут все функции, которые определены для этих значений аргумента.
при данных x будут все функции, которые определены для этих значений аргумента.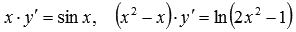 .
. Разбор ЕГЭ 2013 по математике. Задание С1
Разбор ЕГЭ 2013 по математике. Задание С1


