Метод вариации произвольной постоянной для решения линейных неоднородных дифференциальных уравнений первого порядка.

Линейному неоднородному дифференциальному уравнению (ЛНДУ)  соответствует линейное однородное дифференциальное уравнение (ЛОДУ) 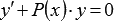 (при Q(x) = 0). Дифференциальное уравнение  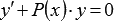оказывается уравнением с разделяющимися переменными.

Возьмем интеграл:

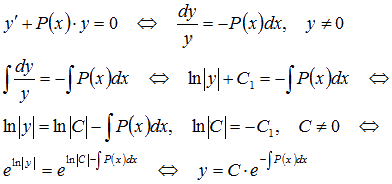
При y=0 дифференциальное уравнение 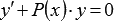 превращается в тождество, поэтому y=0 тоже будет решением (этому варианту соответствует решение  при C=0). Т.о., можно утверждать, что  - общее решение ЛОДУ, где С – произвольная постоянная.

Теперь нам известно, что  является решением ЛОДУ 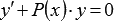. Для вычисления общего решения соответствующего неоднородного уравнения  изменяем постоянную С, т.е., считаем С функцией аргумента x, а не постоянной. Иными словами, берем 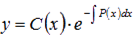 общим решением ЛНДУ.

Значит, подставляя 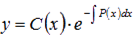 в дифференциальное уравнение , оно обращается в тождество:

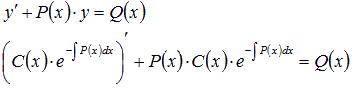
Используем правило дифференцирования произведения:

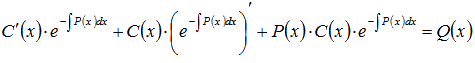
Производная сложной функции  равняется 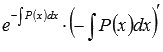. А используя свойства неопределенного интеграла, то:

.

Т.о., имеем возможность сделать такой переход:

.

Уравнение, которое мы получили, является простейшим дифференциальным уравнение первого порядка. Найдя его решение, мы получим функцию C(x) и это даст возможность записать решение начального линейного неоднородного дифференциального уравнения первого порядка как:

.

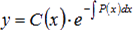Вывод:

Метод вариации произвольной постоянной при решении линейного неоднородного ДУ 1-го порядка состоит из 3-х этапов:

1. В первую очередь определяют общее решение соответствующего ЛОДУ 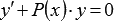 в виде ,
2. Потом варьируем произвольную постоянную С, т.е., заменяем функцией С(x),
3. Конечный шаг: функцию  подставляем в начальное ДУ и из него определяем C(x) и записываем ответ.

Пример применения метода вариации произвольной постоянной:

Найдем решение задачи Коши , y(1) = 3.

Решение.

Другими словами, необходимо найти частное решение линейного неоднородного ДУ  при начальном условии y(1) = 3.

В нашем примере  и Q(x) = x² + 1. В первую очередь находим общее решение линейного однородного дифференциального уравнения. После этого используем метод вариации произвольной постоянной и определяем общее решение ЛНДУ, и находим частное решение, которое ищем.

Общим решением ЛОДУ 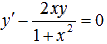 будет семейство функций:

,

где С – произвольная постоянная.

Варьируя произвольную постоянную 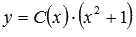 и подставляя эту функцию в начально уравнение получаем:

отсюда 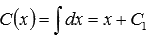, где C₁ – произвольная постоянная.

Тогда, 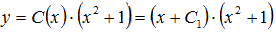 - общее решение неоднородного уравнения.

Теперь необходимо вычислить частное решение, которое удовлетворяло бы исходному условию y(1) = 3.

Т.к. , тогда . Из начального условия, получаем уравнение , из него получаем: .

Значит, искомое решение задачи Коши выглядит так: .