ЕГЭ формулы, шпаргалки - Дифференциальная геометрия. Линии на плоскости.

Линии на плоскости.

Касательным вектором (или вектором скорости) к линии, задаваемой в параметрической форме r = r (t) ≡ (x (t); y (t)), где t пробегает некоторый отрезок, называется вектор:

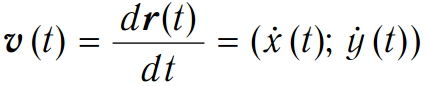
Вектором ускорения называется вектор:

,

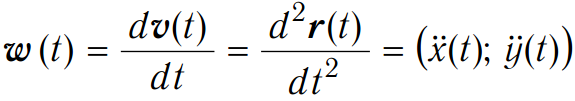Если в качестве параметра t выбрана длина линии l, то | v | = 1; l называют натуральным параметром кривой. 

Кривизной k линии r = r (l) с натуральным параметром l называется модуль вектора ускорения: k = | w (l) |.

Радиусом кривизны линии называется число R = 1/k.

Длина линии, задаваемой в параметрической форме r = r (t) ≡ (x (t); y (t)), от точки (x (t₁); y (t₁)) до точки (x (t₂); y (t₂)):

,

Уравнение касательной к линии x = x (t), y = y (t) в точке t₀:

,

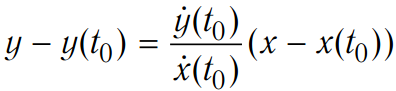Уравнение нормали к линии x = x (t), y = y (t) в точке t₀:

,

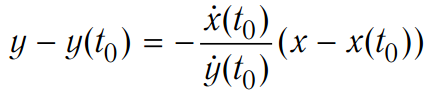Единичный вектор нормали n к кривой x = x (t), y = y (t) с натуральным параметром l:

,

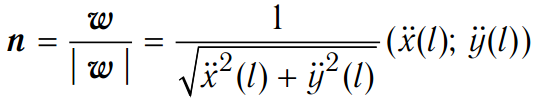Угол между двумя кривыми x = x₁ (t), y = y₁ (t) и x = x₂ (t), y = y₂ (t), пересекающимися при t = t₀:

,

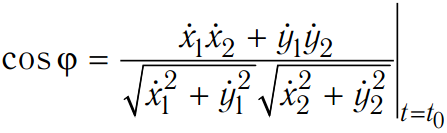Кривизна k линии :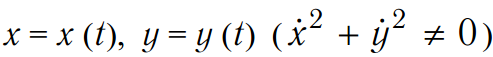

,

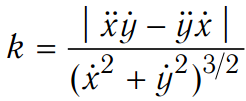Координаты центра круга кривизны линии x = x (t), y = y (t) при t = t₀:

,

Формулы Френе:

.

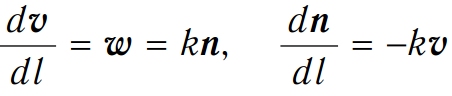Полный список всех формул, шпаргалок для ЕГЭ по математике тут: ЕГЭ математика - формулы, шпаргалки.