Понижение порядка дифференциальных уравнений (ДУ), не содержащих искомую функцию и производных до k–1 порядка, типа 
.
Порядок ДУ можно понизить до n–k при помощи замены переменных 
. В результате замены имеем:
.
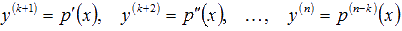После подстановки полученных ответов в заданное уравнение получаем дифференциальное уравнение порядка n–k с неизвестной функцией p(x). После вычисления p(x), функцию y(x) можно вычислить из равенства путем интегрирования k раз подряд.
Пример 1.
Необходимо найти общее решение дифференциального уравнения 
.
Решение.
При помощи замены 
порядок заданного дифференциального уравнения можно понизить с 4-го до 2-го:
,
и исходное однородное дифференциальное уравнение 4-го порядка приводится к ЛОДУ второго порядка с постоянными коэффициентами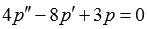 
.
Его характеристическим уравнением является 
, а корнями этого характеристического уравнения оказываются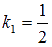 
и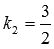 
, тогда, общее решение дифференциального уравнения 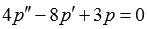принимает вид:
.
Проинтегрировав этот результат два раза, находим искомое общее решение ДУ четвертого порядка:
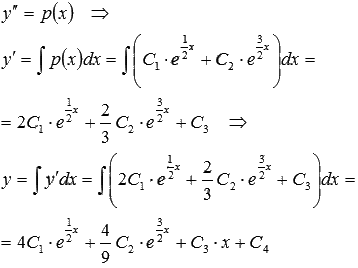
Ответ:
,
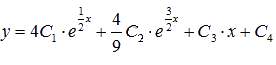где С1, С2, С3 и С4 – произвольные постоянные.
Пример 2.
Нужно вычислить общее решение дифференциального уравнения 3-го порядка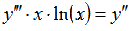 
.
Решение.
Допустим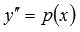 
, значит, 
и исходное дифференциальное уравнение третьего порядка сводится к дифференциальному уравнению с разделяющимися переменными типа 
.
Разделим переменные и проинтегрируем:
Потенцируем выведенное равенство и не забывая, что p(x)=0 тоже оказывается решением, получаем общее решение дифференциального уравнения в виде 
, где C – произвольная постоянная.
Т.к. была введена замена 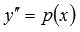, значит,
, тогда,
.
Используем методом интегрирования по частям:
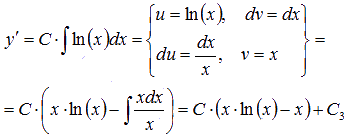
Интегрируем повторно для получения общего решения исходного дифференциального уравнения 3-го порядка:
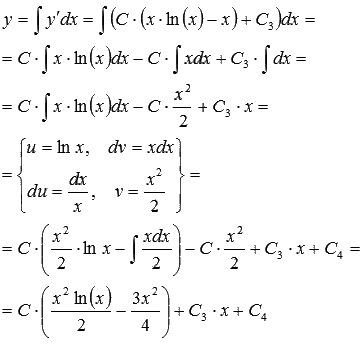
Ответ:
,
где С, С3 и С4 – произвольные постоянные.
Разбор ЕГЭ 2013 по математике. Задание С1
