Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).
Производную определяют как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к 0, если такой предел есть. Функция, которая имеет конечную производную (в некоторой точке), называется дифференцируемой (в данной точке).
Процесс нахождения производной является дифференцированием. Обратный процесс — вычисление первообразной — интегрирование.
Изображение понятия производной:

Рассмотрим взятую наугад внутреннюю точку x0 области определения функции y = f(x).
Разность  где x - тоже внутренняя точка области определения, является приращением аргумента в точке x0.
где x - тоже внутренняя точка области определения, является приращением аргумента в точке x0.
Разность  является приращением функции в точке x0, соответствующим приращению
является приращением функции в точке x0, соответствующим приращению  и обозначают как
и обозначают как  .
.
Производной функции y = f(x) в точке x0 является предел отношения приращения функции к приращению аргумента в этой точке при стремлении приращения аргумента к 0, если такой предел есть и конечен, то есть:

Основные свойства производных.
Если в точке x есть конечные производные функций v = v(x) и u = u(x), тогда в этой точке есть и производные суммы, разности, произведения и частного таких функций, при этом:
1.  ,
,
2.  ,
,
3.  ,
,
4.  при
при  ,
,
5.  ,
,  .
.
1. Производная сложной функции.
Если у функции y = f(x) есть производная в точке x0, а у функции y = g(x) есть производная в точке y0 = f(x0), тогда у сложной функции h(x) = g(f(x)) тоже есть производная в точке x0, при этом:

2. Достаточное условие монотонности функции.
Если во всех точках интервала (a; b) выполняется неравенство:

то функция y = f(x) возрастает на этом интервале.
Если  при
при  то y = f(x) убывает на (a; b).
то y = f(x) убывает на (a; b).
3. Необходимое условие экстремума функции.
Если точка x0 оказывается точкой экстремума функции y = f(x) и в этой точке есть производная  , тогда она равняется 0:
, тогда она равняется 0:

4. Признак максимума функции.
Если функция y = f(x) определена на интервале (a; b), непрерывна в точке  , у нее есть производная
, у нее есть производная  на интервалах
на интервалах  ,
,  и
и  на интервале
на интервале  и
и  , на интервале
, на интервале  , то точка x0 оказывается точкой максимума функции:
, то точка x0 оказывается точкой максимума функции:

5. Признак минимума функции.
Если функция  определена на интервале
определена на интервале  , непрерывна в точке
, непрерывна в точке  , у нее есть производная
, у нее есть производная  на интервалах
на интервалах  , и
, и  , на интервале
, на интервале  и
и  на интервале
на интервале  , то точка x0 оказывается точкой минимума функции:
, то точка x0 оказывается точкой минимума функции:

Правило отыскания наибольшего и наименьшего значений функции.
Чтобы вычислить самое большое и маленькое значения функции, которая имеет на отрезке конечное количество критических точек (точек из области определения, обращающих производную функции в ноль либо не существует), необходимо определить значения функции в каждой критической точке и на концах отрезка и выбрать самое большое и маленькое из полученных чисел.
Определение производной функции.
Пусть в некоторой окрестности точки  определена функция
определена функция  . Производной функции является такое число A, что функцию в окрестности
. Производной функции является такое число A, что функцию в окрестности  можно представить как:
можно представить как:

если A существует.
Определение производной функции через предел.
Пусть в некоторой окрестности точки  определена функция
определена функция  . Производной функции f в точке
. Производной функции f в точке  является предел, если он существует:
является предел, если он существует:

Общепринятые обозначения производной функции в точке .

Обратите внимание, что последнее зачастую обозначает производную по времени (в теоретической механике).
Геометрический и физический смысл производной.
Тангенс угла наклона касательной прямой.
Если у функции  есть конечная производная в точке
есть конечная производная в точке  , тогда в окрестности
, тогда в окрестности  ее можно приблизить линейной функцией:
ее можно приблизить линейной функцией:

Функция  является касательной к f в точке
является касательной к f в точке  . Число
. Число  называется угловым коэффициентом или тангенсом угла наклона касательной прямой.
называется угловым коэффициентом или тангенсом угла наклона касательной прямой.
Скорость изменения функции.
Пусть  — закон прямолинейного движения. Тогда
— закон прямолинейного движения. Тогда  выражает мгновенную скорость движения в момент времени
выражает мгновенную скорость движения в момент времени  . Вторая производная
. Вторая производная  выражает мгновенное ускорение в момент времени
выражает мгновенное ускорение в момент времени 
В общем производная функции  в точке
в точке  выражает скорость изменения функции в точке
выражает скорость изменения функции в точке  , т.е. скорость протекания процесса, который описан зависимостью
, т.е. скорость протекания процесса, который описан зависимостью 
Примеры производных функций.
- Пусть
 . Тогда
. Тогда

- Пусть
 . Тогда если
. Тогда если  то
то

где  обозначает функцию знака. А если
обозначает функцию знака. А если  то
то  , а следовательно
, а следовательно  не существует.
не существует.
Способы задания производных.
- Производная Джексона
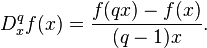
 Разбор ЕГЭ 2013 по математике. Задание С1
Разбор ЕГЭ 2013 по математике. Задание С1


