Тригонометрия. Обратные тригонометрические функции. Арктангенс.

Обратные тригонометрические функции (круговые функции, аркфункции) — математические функции, которые являются обратными к тригонометрическим функциям.

Арктангенс - обозначение: arctg x или arctan x.

Арктангенс (y = arctg x) – обратная функция к tg (x = tg y), которая имеет область определения 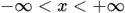 и множество значений 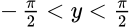. Другими словами возвращает угол по значению его tg.

Функция y = arctg x непрерывна и ограничена на всей своей числовой прямой. Функция y = arctg x является строго возрастающей.

Свойства функции arctg .

• 
• 
•  при x > 0,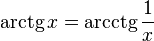
• 

График функции y = arctg x .

График арктангенса получают из графика тангенса, меняя местами оси абсцисс и ординат. Чтоб избавиться от многозначности, множество значений ограничивают интервалом , на нем функция монотонна. Это определение называется главным значением арктангенса.

Получение функции arctg .

Есть функция y = tg x. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arctg x не является функцией. Поэтому рассматриваем отрезок, на котором она только возрастает и принимает все значения лишь 1 раз — 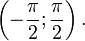. На таком отрезке y = tg x только возрастает монотонно и принимает все значения лишь 1 раз, то есть, на интервале  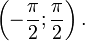есть обратная y = arctg x, график ее симметричен графику y = tg x на отрезке  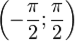относительно прямой y = x.