Уравнения. Иррациональные уравнения.

Иррациональными уравнениями – это уравнения, имеющие неизвестное под знаком радикала.

Например:

Рассмотрим иррациональных уравнений, на примере уравнений, содержащих квадратные радикалы.

Квадратные корни извлекаются из неотрицательных чисел.

Выражения вида корень из трех   , квадратный корень из пяти 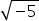 не имеют смысла (объяснение этому можно посмотреть здесь).

При извлечении корня из положительного числа его значение обязательно будет также положительным числом.

Например, 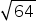    = 8, а нe - 8;  = 1,73205 а не - 1,73205 и т.д.

Рассмотрим решение типичных иррациональных уравнений.

Например, задано решить уравнение вида:

Известно, что квадратные корни извлекаются только из неотрицательных чисел, поэтому допустимые значения искомой величины х должны удовлетворять требованиям составляемой системы:

Первое неравенство показывает, что х ≥ 2, второе что х ≤ 1. Очевидно, что одновременно эти два условия не выполнимы, именно поэтому множество допустимых значений искомой величины х пустое, т.е. не содержит ни одного действительного числа.

При нахождении решения иррационального уравнения, необходимо удостовериться, что множество допустимых значений искомой величины существует, т.е. является допустимым для искомой величины, в противном случае уравнение не имеет корней.

Например:

Ни один из найденных корней уравнения 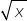  и 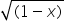 не может быть числом отрицательным, поэтому ни при каких значениях действительных величины х сумма этих неотрицательных корней не может равняться –2, следовательно, решения данное уравнение не имеет.