Формула Эйлера.

Формула Эйлера устанавливает взаимосвязь меж экспоненциальной функцией 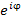 и тригонометрическими функциям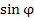и  и  на множестве комплексных чисел:

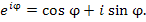    (1)

где e — 1-на из самых важных математических констант, которая определяется при помощи формулы:

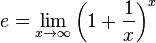
i — мнимая единица.

Другими словами формула Эйлера заявляет, что для всякого действительного числа и комплексного числа x выполняется равенство, указанное выше.

Доказательство формулы Эйлера.

Доказательство формулы Эйлера основывается на представлении этих функций как степенные ряды и при первом чтении может быть опущено без вреда для понимания дальнейшего изъяснения.

     Отметим, что 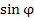 и  - это, соответственно, вещественная и мнимая части экспоненциальной функции :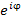

     (2)

     (3)

Заменим в формуле Эйлера :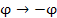

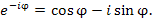
Выполняем почленное сложение и вычитание выражений в обеих частях равенств (1) и (3), получаем:

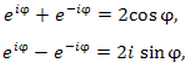
следовательно:

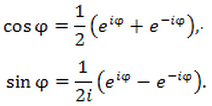
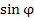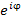Т.о., тригонометрические функции  и  представлены как линейные комбинации экспоненциальных функций  и .

tg φ выражаем через :

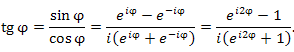
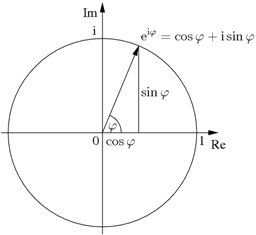
Геометрический смысл формулы Эйлера.

Производные формулы Эйлера.

С помощью формулы Эйлера определяют функции sin и cos:

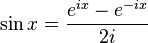
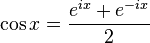
Дальше вводят понятие тригонометрических функций комплексной переменной. Допустим x=iy, значит:

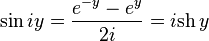
Известное тождество Эйлера, которое связывает 5 основных математических констант:

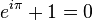
является частным случаем формулы Эйлера при x=π.