Формула Ньютона — Лейбница (основная теорема анализа) дает связь между 2-мя операциями: взятием интеграла Римана и определением первообразной. Формула Ньютона-Лейбница - важнейшая формула интегрального исчисления.
Пусть f непрерывна на отрезке [a,b] и Φ, ее всякая первообразная на этом отрезке, тогда имеет место равенство:
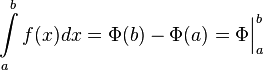
Эта формула верна для всех функций f(x), непрерывной на отрезке [а, b], Φ - первообразная для f(x). Т.о., что бы вычислить конкретный интеграл, необходимо найти любую первообразную Φ функции f(x), определить ее значения в точках a и b и вычислить Φ (b) – F(a).
Рассмотрим применение формулы Ньютона-Лейбница на конкретном примере:
Вычислить интеграл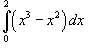 
.
Решение:
Применяем формулу Ньютона-Лейбница:
Разбор ЕГЭ 2013 по математике. Задание С1
