Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формулу Тейлора функции зачастую используют доказывая теоремы в дифференциальном исчислении.
Формула Тейлора:
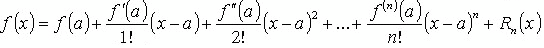
где Rn(x) - остаточный член формулы Тейлора.
Формула Тейлора для многочлена.
Есть функция ƒ(х) и многочлен Рn(х) степени n:
ƒ(х)=Рn(х)=а0+а1х+а2х2+...+аnхn.
Преобразуем этот многочлен в многочлен степени n относительно разности х-х0, где х0 — любое число, то есть представим Рn(х) как:
Рn(х)=А0+A1(x-х0)+А2(х-х0)2+...+Аn(х-х0)n (1)
Для определения коэффициентов А0, А1,..., Аn дифференцируем n раз равенство (1):
Р'n(х)=А1+2А2(х-x0)+3A3(x-x0)2+...+nAn(x-x0)n-1,
Рn''(х)=2А2+2•3А3(х-х0)+...+n(n-1)Аn(х-х0)n-2,
Рn"'(х)=2•3А3+2•3•4А4(х-х0)+...+n(n-1)(n-2)Аn(х-х0)n-3,
- - - - - - - - - - - - - - - - - -
Рn(n)(х)=n(n-1)( n-2)...2•1Аn
Подставляем х=х0 в равенства, которые мы получили и равенство (1), получаем:

Подставляем определенные значения A0, A1, ..., An в равенство (1), получаем разложение многочлена n-й степени Рn(х) по степеням (х-х0):

Эта формула является формулой Тейлора для многочлена Рn(х) степени n.
Формула Тейлора для произвольной функции.
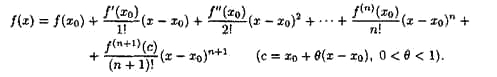
Остаточный член формулы Тейлора.
В форме Лагранжа:

В форме Коши:

 Разбор ЕГЭ 2013 по математике. Задание С1
Разбор ЕГЭ 2013 по математике. Задание С1


