Алгоритм определения общего решения ЛОДУ 2-го порядка с постоянными коэффициентами 
.
1. Запишем характеристическое уравнение k2 + p ⋅ k + q = 0.
2. Найдем корни характеристического уравнения k1 и k2.
3. Учитывая значения корней характеристического уравнения, запишем общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами как:
, если 
;
, если 
;
, если 
.
Что бы лучше все понять, разберем примеры для всех случаев.
Пример 1.
Найдем общее решение ЛОДУ 2-го порядка с постоянными коэффициентами 
.
Решение.
Для начала записываем характеристическое уравнение k2 + 4 ⋅ k + 4 = 0 и находим его корни:
После проведения рассчетов у нас получилось 2 совпадающих корня, а, значит, общее решение выглядит так:
.
Пример 2.
Найдем общее решение ДУ 
.
Решение.
У нас есть линейное однородное дифферениальное уравнение второго порядка с постоянными коэффициентами. Записываем характеристическое уравнение и находим корни этого уравнения:
Корни в этом случае являются действительными и различными, значит, общее решение однородного уравнения будет выглядеть так:
.
Пример.
.Решение.
Характеристическое уравнение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами выглядит так: k2 - k + 3 = 0. Вычислим корни этого уравнения:
Отсюда получено два комплексно сопряженных корней характеристического уравнения, значит, общее решение исходного уравнения выражаем так:
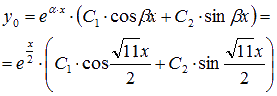
Разбор ЕГЭ 2013 по математике. Задание С1
