ЕГЭ формулы, шпаргалки - Свойства определенного интеграла.

Свойства определенного интеграла.

1. ,

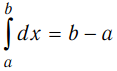2. Если функция f(x) интегрируема на [a, b], то функция f(x) интегрируема и на отрезках [a, c], [c, b] (a - c - b) и .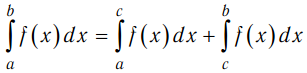

3. Если функция f(x) интегрируема на [a, b], то .

4. Если функция f(x) интегрируема на [a, b], то и функция |f(x)| интегрируема на [a, b] и .

5. Если функция f(x) интегрируема на [a, b], то и функция kf(x) (k = const) интегрируема на [a, b] и .

6. Если функции f(x) и g(x) интегрируемы на [a, b], то и функции f(x) + g(x) и f(x) ⋅ g(x) интегрируемы на [a, b] и .

7. Если функции f(x) и g(x) интегрируемы на [a, b] и f(x) . g(x) на [a, b], то .

Первая теорема о среднем.

Если функции f(x) и g(x) интегрируемы на [a, b], m - f(x) - M и если g(x) не меняет знак на [a, b], то существует такое число µ∈ [m, M], что .

Вторая теорема о среднем.

Если функция f(x) непрерывна, а g(x) монотонна и непрерывно дифференцируема на [a, b], то существует такое число ξ∈ [a, b], что .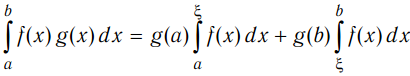

Формула Ньютона - Лейбница.

Если функция f(x) определена и непрерывна на [a, b] и F ′(x) = f(x), то .

Формула замены переменной.

Если функция f(z) непрерывна на [a, b], а функция z = g(x) непрерывна и имеет непрерывную производную на [α; β]; a = g(α), b = g(β), a - g(x) - b, то .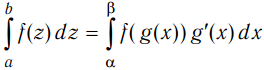

Интегрирование по частям.

Если функции f(x) и g(x) непрерывны на [a, b] вместе со своими первыми производными, то 

.

Интегральное неравенство Минковского.

Если функции f(x) и g(x) интегрируемы на [a, b], 1 < p < +∞, то 

.

Интегральное неравенство Гёльдера.

Если функции f(x) и g(x) интегрируемы на [a, b], 1 < p < +∞ , то

.

При p = q = 2 неравенство Гёльдера превращается в неравенство Коши.

Интеграл с переменным верхним пределом.

Если функция f(x) непрерывна на [a, b], то функция  

непрерывна на [a, b].

Если функция f(x) интегрируема на [a, b] и непрерывна в точке x₀b₀ ∈ [a, b], то функция  дифференцируема в точке x₀ и F ′(x₀) = f(x₀).

Полный список всех формул, шпаргалок для ЕГЭ по математике тут: ЕГЭ математика - формулы, шпаргалки.