Метод вращений. Как и в методе Гаусса, целью прямого хода преобразований в методе вращений является приведение системы линейных уравнений к треугольному виду методичным обнулением поддиагональных элементов сначала 1-го столбца, далее 2-го и так далее.
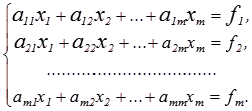
Допустим с1 и s1 – ненулевые числа. Умножаем 1-е уравнение системы на с1, 2-е на s1 и складываем их; уравнением, которое мы получили, заменяем 1-е уравнение системы. Далее 1-е уравнение начальной системы нужно умножить на – s1, 2-е – на c1 и итогом этого заменяем 2-е уравнение. Т.о., первые 2 уравнения заменяем уравнениями:

На параметры с1 и s1 наложим 2 условия:
- условие исключения х1 из второго уравнения и
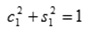
- условие нормировки
Получаем:

Эти числа можно истолковать как cos и sin некоторого угла α1 (поэтому метод так и называется - все шаги этого преобразования рассматриваются как вращение расширенной матрицы системы в плоскости индекса, который обнуляется).
После преобразований получаем систему:

где

Теперь 1-е уравнение системы заменяем полученным, результатом сложения итогов умножения 1-го и 3-го уравнений соответственно на:

а 3-е – уравнением, которое получим после сложения результатов умножения уравнений соответственно на – s2 и с2. Получаем систему:

где:

Выполняя преобразование m-1 раз, приходим к системе:

Вид системы, которую мы получили, такой же, как и после 1-го этапа преобразований методом Гаусса. У этой системы следующие свойства: длина всех векторов-столбцов расширенной матрицы остается такая же, как у исходной матрицы. То есть, при выполнении преобразований не роста элементов нет.
Далее, по этому же алгоритму преобразуем матрицу:

и так далее.
В итоге m-1 этапов прямого хода система приведется к треугольному виду:
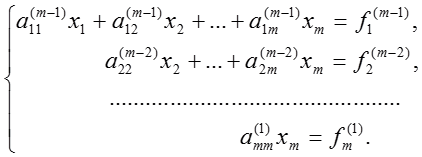
Определение неизвестных такое же как и в обратном ходе метода Гаусса.
Треугольная, или, трапециевидная структура последней системы дает нам поочередно 1 за другим вычислить значения неизвестных, начиная с последнего:
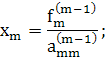


 Разбор ЕГЭ 2013 по математике. Задание С1
Разбор ЕГЭ 2013 по математике. Задание С1


