Дифференцирование – определение производных и дифференциалов всех порядков от функции одной переменной и частных производных и дифференциалов, кроме того, полных дифференциалов от функций большинства переменных.
Доказательство правила дифференцирования произведения 2-х функций:
Записываем предел отношения приращения произведения функций к приращению аргумента. Учитываем, что:
и 
(приращение функции стремится к 0 при приращении аргумента, который стремится к 0).
Правило доказано.
Теперь рассмотрим на нескольких примерах вышеуказанное правило.
Пример 1.
Продифференцируем функцию:
.
В этом примере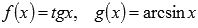 
. Применим правило производной произведения:
Смотрим таблицу производных основных элементарных функций и находим решение:
Пример 2.
Найдем производную функции:
.
В данном примере 
. Значит:
Теперь посмотрим на вариант определения производной произведения 3-х функций. По такой системе дифференцируют произведение 4-х, и 5-ти, и 25-ти функций.
Пример 3.
Продифференцируем функции:
.
Исходим из правила дифференцирования произведения 2-х функций. Функцией f(x) считаем произведение (1+x)sinx, а функцией g(x) возьмем lnx:
Что бы определить 
снова применяем правило производной произведения:
Воспользуемся правилом производной суммы и таблицей производных:
Подставляем результат, который мы получили:
Из выше описанного видно, иногда нужно применять не только одно правило дифференцирования на одном примере. Тут важно делать все последовательно и внимательно.
Пример 4.
Найдем производную функции:
.
Функция является разностью выражений 
и 
, значит:
В первом выражении выносим 2-йку за знак производной, а во 2-м выражении используем правило дифференцирования произведения:
Разбор ЕГЭ 2013 по математике. Задание С1
