Относительность Галилея.

Принцип относительности Галилея гласит:

Механические явления протекают одинаково во всех инерциальных системах отсчета,  т. е. описывающие их законы динамики одинаковы. Поэтому все инерциальные системы отсчета равноправны.

Это значит, что уравнения, выражающие законы механики, не меняются при преобразованиях Галилея.

Преобразования Галилея заключаются в преобразовании координат  и времени t движущейся материальной точки при переходе от одной инерциальной системы отсчета к другой:

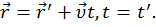
Для координаты x это выражается так:

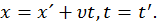
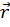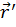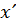Здесь  и - радиус-векторы,  и  - координаты точки в двух инерциальных системах отсчета, а υ – относительная скорость движения этих двух инерциальных систем отсчета. Время не изменяется при переходе из одной инерциальной системы отсчета в другую: принцип относительности Галилея основан на представлениях об абсолютном времени и абсолютном пространстве. Это означает, что во всех инерциальных системах отсчета события протекают одинаково (одновременно).

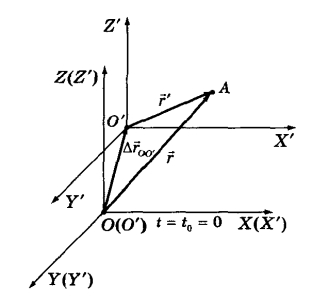
В некоторый начальный момент времени t₀ = 0 возьмем одну из систем координат К (XYZ) и совместим с подвижной – K´(X´Y´Z´) . Зафиксируем систему K. В любой последующий момент времени положение некоторой точки А, движущейся относительно обеих систем координат, определяется в системе K радиус-вектором 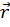, а в системе K´ - радиус-вектором 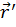. Вектор, соединяющий начало координат О неподвижной системы координат с началом коорди­нат О´ подвижной системы, равен вектору переме­щения системы K´ относительно K: 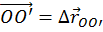. Согласно правилу сложения векторов, . Выразив вектор перемещения через скорость движения системы K´ относительно K, получим . Исходя из этого,

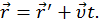
Из этого уравнения вытекает закон сложения скоростей:

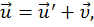
где  - скорости точки относительно систем K и K´ соответственно. Дифференцируем по времени это выражение и получим w = w´. Это значит, что ускорение точки в данный момент времени одинаково относительно любой из систем, неускоренно движущихся относительно друг друга.

Галилей на основании наблюдений сформулировал классический принцип относи­тельности, согласно которому законы механики одинаковы в любых инерциальных системах отсчета. То есть, уравнения движения относительно любых инерциальных систем совпадают друг с другом. Это значит, что уравнение mw = F эквивалентно уравнению m´w´ = F´.

Из принципа Галилея следует, что F = F´, т. е. силы, действующие на точку, неизменны при переходе от одной инерциальной системы к другой, также инерциальной системе.

Следовательно, все величины, входящие в уравнение Ньютона, не изменяются при преобразовании от одной инерциальной системы к другой инерциальной системе.