Мнимая единица — в основном комплексное число, квадрат которого равняется отрицательной единице: 
.
Число 
называется мнимой единицей.
Мнимая единица не относится к привычному нам множеству действительных чисел, а используется для расширения этого множества.
Мнимая единица — это число, у которого квадрат равняется минус единице. То есть i — это одно из решений уравнения:
или 
.
И тогда его вторым решением уравнения будет 
, что можно проверить подстановкой.
Комплексная плоскость. Все точки на плоскости соответствуют комплексному числу. Координаты a и b соответствуют действительной и мнимой части комплексного числа.
Примеры расчетов с мнимой единицей.
;
;
;
.
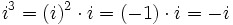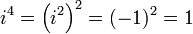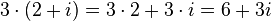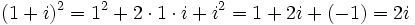Интересно то, что все многочлены имеют корни, если брать в расчет мнимую единицу, если точнее, количество корней равняется степени многочлена, с точностью до кратности корней.
Например:
Степени мнимой единицы .
Степени i повторяются циклично:
Это можно записать для любой степени таким образом:
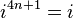
где n — всякое целое число.
Отсюда: 
, где mod 4 это остаток от деления на 4.
Число 
оказывается вещественным числом:
Корни из мнимой единицы .
В поле комплексных чисел корень n-ой степени имеет n решений. На комплексной плоскости корни из мнимой единицы расположены в вершинах правильного n-угольника, который вписан в окружность единичного радиуса.
Это следует из формулы Муавра и того, что мнимую единицу можно представить в тригонометрическом виде:
В частности, 
и 
Кроме того, корни из мнимой единицы можно представить в показательном виде:
Корни квадратные из мнимой единицы.
Корни кубические из мнимой единицы (вершины треугольника).