В соответствии со способами задания координат, движение точки можно описать координатным или векторным способом.
Рассмотрим координатный способ задания движения.
Допустим, движение точки задано функциями всех трех ее координат от времени:
x = x(t), y = y(t), z = z(t).
Это кинематеческие уравнения движения точки, записанные в координатной форме. Все три уравнения скалярны.
По этим уравнениям для каждого момента времени t можно определить координаты точки и указать ее положение в пространстве. При множестве значений t получим множество положений точки в пространстве – траекторию точки. Иными словами, уравнения движения являются уравнениями траектории точки в параметрической форме, где в качестве параметра служит время t. Для получения уравнения траектории в виде зависимости между координатами точки достаточно из вышеприведенных уравнений движения исключить время.
При векторном способе задания движения изменение положения точки задано ее радиус-вектором как функцией от времени:
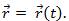
Зная это уравнение, для любого момента времени можно рассчитать радиус-вектор точки – определить ее положение (как и при координатном способе). Следовательно, задание трех скалярных уравнений равносильно заданию одного векторного уравнения.
Для каждого случая движения вид уравнений будет вполне определенным.
Электромагнитные колебания
