Прогрессии (арифметическая, геометрическая), формулы.

Прогрессия — последовательность величин, каждая последующая из них находится в некоторой, общей для всей прогрессии, зависимости от предыдущей.

Арифметическая прогрессия .

Арифметическая прогрессия - это ряд чисел, в котором все член получаются из предыдущего методом добавления к нему 1-го и того же числа d, которое называется разностью арифметической прогрессии.

Или другими словами: арифметическая прогрессия — численная последовательность, которая имеет вид:

,

т.е. последовательность чисел (членов прогрессии), в которой числа, начиная со 2-го, получаются из предыдущего путем добавления к нему постоянного числа  (шаг либо разность прогрессии):

Всякий (n-й) член прогрессии можно вычислить с помощью формулы общего члена:

Арифметическая прогрессия - это монотонная последовательность. При  она возрастает, а при  — убывает. Если , то последовательность - стационарная. Это следуют из соотношения  для членов арифметической прогрессии.

Свойства арифметической прогрессии.

1. Общий член арифметической прогрессии.

Член арифметической прогрессии с номером  можно найти с помощью формулы:

,

 где  — 1-й член прогрессии,  — разность прогрессии.

2. Характеристическое свойство арифметической прогрессии.

Последовательность   - это арифметическая прогрессия  для элементов этой прогрессии выполняется условие:

.

3. Сумма 1-х  членов арифметической прогрессии.

Сумму 1-х   членов арифметической прогрессии  можно найти с помощью формул:

,

где  — 1-й член прогрессии, 

 — член с номером , 

 — число суммируемых членов.

,

где  — 1-й член прогрессии, 

 — разность прогрессии, 

 — число суммируемых членов.

4. Сходимость арифметической прогрессии.

Арифметическая прогрессия  является расходящейся при  и сходящейся при . При этом:

5. Связь между арифметической и геометрической прогрессиями.

Есть  — арифметическая прогрессия с разностью , где число . Тогда последовательность, которая имеет вид  является геометрической прогрессией, имеющей знаменатель .

Примеры арифметических прогрессий.

1. Натуральный ряд 1, 2, 3, 4, 5,… является арифметической прогрессией, в которой 1-й член , а разность .

1, -1, -3, -5, -7 — первые пять членов арифметической прогрессии, в которой  и .

2. Если каждый элемент некоторой последовательности имеет такую же величину, как и остальные элементы этой системы и равен некоторому числу , тогда это является арифметической прогрессией, в которой  и . В частности,  является арифметической прогрессией с разностью .

3. Сумма 1-х  натуральных чисел выражают формулой:

.

Геометрическая прогрессия.

Геометрическая прогрессия — это последовательность чисел  (членов прогрессии), в которой каждое число, начиная со 2-го, получают из предыдущего путем умножения его на определённое число  (знаменатель прогрессии), где , : .

Или другими словами: геометрическая прогрессия - это численная последовательность, каждое из чисел равняется предыдущему, умноженному на определенное постоянное число q для данной прогрессии, которое называется знаменателем геометрической прогрессии.

Каждый член геометрической прогрессии можно вычислить при помощи формулы:

Когда  и , значит, прогрессия возрастает , когда 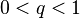, значит, прогрессия убывает, а при  — знакочередуется.

Название геометрическая прогрессия взяла из своего характеристического свойства:

т.е. все члены равны среднему геометрическому их соседей.

Свойства геометрической прогрессии.

1. Логарифмы членов геометрической прогрессии (если они определены) образуют арифметическую прогрессию:

2. Произведение 1-х n членов геометрической прогрессии рассчитывают при помощи формулы:

,

3. Произведение элементов геометрической прогрессии, начиная с k-ого члена, и заканчивая n-ым членом, рассчитывают при помощи формулы:

4. Сумма n 1-х членов геометрической прогрессии:

5. Если , то  при , и при .

Примеры геометрических прогрессий.

1. Последовательность площадей квадратов, в которой каждый последующий квадрат получают соединением середин сторон предыдущего — геометрическая прогрессия со знаменателем ½, не имеющая предела. Площади образующихся на каждом этапе треугольников тоже образуют нескончаемую геометрическую прогрессию со знаменателем ½, сумма которой равняется площади начального квадрата.

2. Последовательность числа зёрен на клетках в задаче о зёрнах на шахматной доске.

3. 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 — прогрессия со знаменателем 2 из 13 членов.

4. 50; −25; 12,5; −6,25; 3,125; … — нескончаемо убывающая прогрессия со знаменателем -½.

5.  — геометрическая прогрессия со знаменателем равным единице (и арифметическая прогрессия с шагом 0).

И как заключение:

Арифметическая прогрессия, формулы.

Формула n-го члена:

Формулы суммы n первых членов:

Геометрическая прогрессия, формулы.

Формула n-го члена:

Формулы суммы n первых членов:

Сумма бесконечной прогрессии: