Основы теории вероятностей. Дисперсия случайной величины.

Дисперсия случайной величины характеризует степень разброса случайной величины около ее математического ожидания, то есть её отклонения от математического ожидания.

Если случайная величина ξ имеет математическое ожидание M_ξ, то дисперсией случайной величины ξ выражается так:

D_ξ = M(_ξ - M_ξ )².

Из этого следует, что                                        D_ξ = M(_ξ - M_ξ )2= M_ξ 2 - M(_ξ)².

Эта универсальная формула отлично применима как для дискретных случайных величин, так и для непрерывных. Величина M_ξ ² больше для дискретных и непрерывных случайных величин соответственно вычисляется по формулам:

, .

Для вычисления степени разброса значений случайной величины зачастую используют среднеквадратичное отклонение , связанное с дисперсией соотношением .

Свойства дисперсии случайной величины.

• Дисперсия каждой случайной величины неотрицательна:

• Если дисперсия случайной величины конечна, то конечно и её математическое ожидание;
• Если случайная величина = константе, то её дисперсия = 0:

Верно и обратное утверждение: если , то  почти везде;

• Дисперсия суммы двух случайных величин равна:

,

•   — их ковариация;
• Для дисперсии произвольной линейной комбинации нескольких случайных величин соответствует следующая формула:

,

где

• Например,  для любых независимых или некоррелированных случайных величин, потому что ковариации этих случайных величин равны нулю;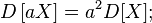
• 
• 
• 

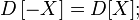
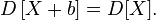
Пример. Как найти математическое ожидание и дисперсию.

Предположим, случайная величина X имеет стандартное непрерывное равномерное распределение на [0,1], т.е. её плотность вероятности задана следующим равенством:

Из этого следует, что математическое ожидание квадрата случайной величины можно выразить таким образом:

и формула математического ожидания случайной величины выглядит так:

Следовательно, дисперсию случайной величины найдем по формуле:

.