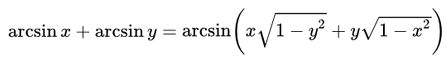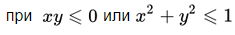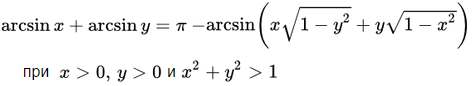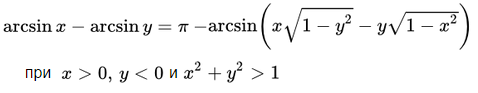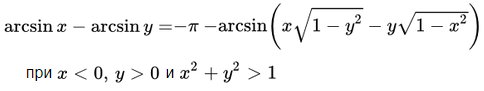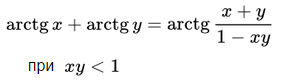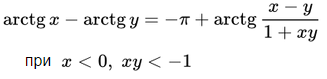Обратные тригонометрические функции (круговые функции, аркфункции) — математические функции, которые являются обратными к тригонометрическим функциям.
К ним обычно относят 6 функций:
- арксинус (обозначение: arcsin x; arcsin x — это угол, sin которого равен x),
- арккосинус (обозначение: arccos x; arccos x — это угол, косинус которого равняется x и так далее),
- арктангенс (обозначение: arctg x или arctan x),
- арккотангенс (обозначение: arcctg x или arccot x или arccotan x),
- арксеканс (обозначение: arcsec x),
- арккосеканс (обозначение: arccosec x или arccsc x).
Арксинус (y = arcsin x) – обратная функция к sin (x = sin y), которая имеет область определения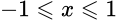 
и множество значений 
. Другими словами возвращает угол по значению его sin.
Арккосинус (y = arccos x) – обратная функция к cos (x = cos y), которая имеет область определения 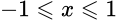и множество значений 
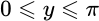. Другими словами возвращает угол по значению его cos.
Арктангенс (y = arctg x) – обратная функция к tg (x = tg y), которая имеет область определения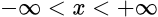 
и множество значений 
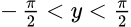. Другими словами возвращает угол по значению его tg.
Арккотангенс (y = arcctg x) – обратная функция к ctg (x = ctg y), которая имеет область определения 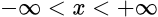и множество значений 
. Другими словами возвращает угол по значению его ctg.
arcsec - арксеканс, возвращает угол по значению его секанса.
arccosec - арккосеканс, возвращает угол по значению его косеканса.
Когда обратная тригонометрическая функция не определяется в указанной точке, значит, ее значение не появится в итоговой таблице. Функции arcsec и arccosec не определяются на отрезке (-1,1), а arcsin и arccos определяются только на отрезке [-1,1].
Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции прибавлением приставки «арк-» (от лат. arcus — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции связывают с длиной дуги единичной окружности (либо углом, который стягивает эту дугу), которая соответствует тому либо другому отрезку.
Иногда в зарубежной литературе, как и в научных/инженерных калькуляторах, используют обозначениями вроде sin−1, cos−1 для арксинуса, арккосинуса и тому подобное, — это считается не полностью точным, т.к. вероятна путаница с возведением функции в степень −1 («−1» (минус первая степень) определяет функцию x = f-1(y), обратную функции y = f (x)).
Основные соотношения обратных тригонометрических функций.
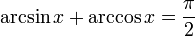
Здесь важно обратить внимание на интервалы, для которых справедливы формулы.
Формулы, связывающие обратные тригонометрические функции.
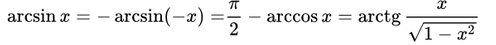
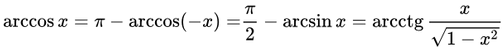
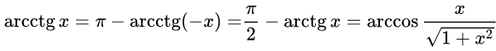
Обозначим любое из значений обратных тригонометрических функций через Arcsin x, Arccos x, Arctan x, Arccot x и сохраним обозначения: arcsin x, arcos x, arctan x, arccot x для их главных значений, тогда связь меж ними выражается такими соотношениями:
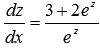
где k – всякое целое число. При k = 0 у нас есть главные значения.
Формулы суммы и разности обратных тригонометрических функций.
