Если величины х и у обратно пропорциональны, то функциональная зависимость между ними выражается уравнением:
,
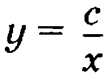где с это постоянная величина.
График, характеризующий обратную пропорциональность это кривая линия, состоящая из двух «ветвей». Например, функция y = 2/x изображается кривой, ветви которой АВ и А'В' показаны на рисунке. Остальные линии характеризуют графики функции у = с/х при значении с = 1 и - 1.
Изображенные кривые называются равносторонними гиперболами и получаются при пересечении конуса с прямым углом при вершине плоскостями, параллельными оси.
|
|
Математические калькуляторы
|
|
Математические калькуляторы: корни, дроби, степени, уравнения, фигуры, системы счисления и другие калькуляторы.
|
|
Математические калькуляторы
|
|
|
|
|
Калькуляторы по алгебре
|
|
Решения, подсказки и учебник линейной алгебры онлайн (все калькуляторы по алгебре).
|
|
Калькуляторы по алгебре
|
|
|
|
|
|
Математика 4,5,6,7,8,9,10,11 класс, ЕГЭ, ГИА
|
|
Основная информация по курсу математики для обучения и подготовки в экзаменам, ГВЭ, ЕГЭ, ОГЭ, ГИА
|
|
Математика 4,5,6,7,8,9,10,11 класс, ЕГЭ, ГИА
|
|
|
|
|
Пропорциональные величины.
|
|
Когда переменные величины х и у пропорциональны, то зависимость между ними имеет вид: y = mx , где m - постоянная величина или иначе коэффициент пропорциональности .
|
|
Пропорциональные величины.
|
|
|
|
|
Разбор ЕГЭ 2013 по математике. Задание С1
