ЕГЭ формулы, шпаргалки - Дифференцирование функций комплексного переменного.

Условия Коши – Римана.

Чтобы однозначная в области G функция комплексного переменного была аналитической в G, необходимо и достаточно, чтобы ее действительная и мнимая части были дифференцируемыми функциями как функции двух действительных переменных и удовлетворяли условиям Коши – Римана в области G:

в декартовых координатах: ,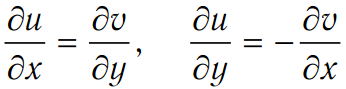

в полярных координатах: .

Функция f(z), дифференцируемая в некоторой области G, является аналитической в этой области. Из дифференцируемости функции в точке z₀ не следует ее аналитичность в этой точке.

Правила вычисления производных функций комплексного переменного формально совпадают с правилами вычисления производных для функций действительного переменного.