ЕГЭ формулы, шпаргалки - Аналитическая геометрия. Плоскость.

Общее уравнение плоскости в декартовой системе координат:

.

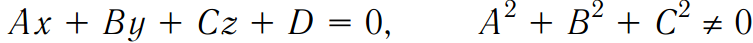Уравнение плоскости в отрезках:

,

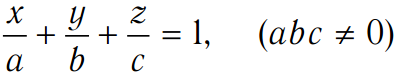(a; 0; 0), (0; b; 0), (0; 0; c) — точки пересечения плоскости с осями Ox, Oy и Oz соответственно.

Нормальное уравнение плоскости:

,

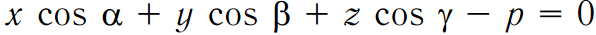где — компоненты вектора единичной длины, перпендикулярного плоскости, p — расстояние от начала координат до плоскости.

Коэффициенты общего и нормального уравнений плоскости связаны равенствами:

,

(знак λ противоположен знаку D).

Параметрическое уравнение плоскости, проходящей через точку (x₀, y₀, z₀) и содержащей неколлинеарные векторы a = (a₁; a₂; a₃) и b= (b₁; b₂; b₃) (u, v — параметры):

x = x₀ + a₁u + b₁v,

y = y₀ + a₂u + b₂u,

z = z₀ + a₃u + b₃v.

Компоненты векторов a и b связаны с коэффициентами A, B, C:

.

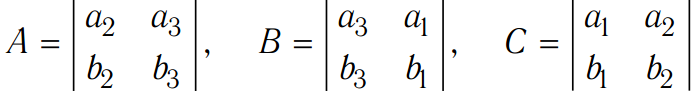Уравнение плоскости, проходящей через три заданные точки (x_i; y_i; z_i) (i = 1, 2, 3), не лежащие на одной прямой:

.

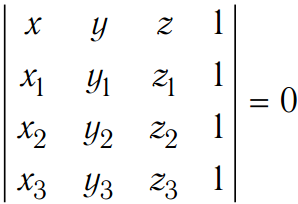Уравнение плоскости, проходящей через заданную точку (x₀, y₀, z₀) и перпендикулярной вектору n = (A; B; C):

A(x – x₀) + B(y – y₀) + C(z – z₀) = 0.

Необходимое и достаточное условие параллельности плоскостей A_ix + B_iy + C_iz + D_i = 0 (i = 1, 2):

A₁ = λA₂, B1 = λB₂, C₁ = λC₂.

Необходимое и достаточное условие перпендикулярности плоскостей: 

A₁ A₂ + B₁B₂ + C₁C₂ = 0.

Расстояние от точки (x₀; y₀; z₀) до плоскости Ax + By + Cz + D = 0:

.

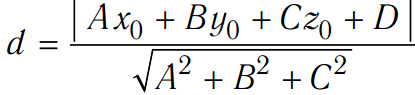Расстояние между двумя параллельными плоскостями Ax + By + Cz + D₁ = 0 и Ax + By + Cz + D₂ = 0:

,

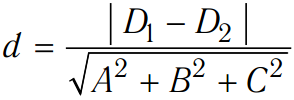Угол между плоскостями Aix + Biy + Ciz + Di = 0 (i = 1, 2):

.

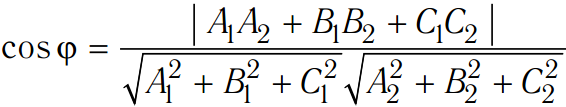Полный список всех формул, шпаргалок для ЕГЭ по математике тут: ЕГЭ математика - формулы, шпаргалки.