Проанализируем расположение квадрата на координатной плоскости.

В общем случае уравнение квадрата в декартовой (прямоугольной) системе координат принимает вид:

 

׀х - а ׀+ ׀ у - b ׀≤ d / 2,

 

где точка О`(a;b) – точка пересечения диагоналей квадрата;

d – длина диагонали квадрата.

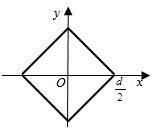
Уравнение квадрата в декартовой системе координат.

 

В частном случае, когда точка О(0;0) - начала координат, является одновременно и точкой пересечения диагоналей квадрата, уравнение квадрата принимает вид:

 

׀х  ׀+ ׀ у ׀≤ d / 2,

 

где d– длина диагонали квадрата.

Уравнение квадрата в декартовой системе координат.