Предел функции.

Предел функции – число a будет пределом некоторой изменяемой величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a.

Или другими словами, число A является пределом функции y = f (x) в точке x₀, если для всякой последовательности точек из области определения функции, не равных x₀, и которая сходится к точке x₀ (lim x_n = x0), последовательность соответствующих значений функции сходится к числу A.

График функции, предел которой при аргументе, который стремится к бесконечности, равен L:

Предел функции по Гейне.

Значение А является пределом (предельным значением) функции f (x) в точке  x₀ в случае, если для всякой последовательности точек , которая сходится к  x₀, но которая не содержит  x₀ как один из своих элементов (т.е. в проколотой окрестности  x₀), последовательность значений функции сходится к A.

Предел функции по Коши.

Значение A будет являться пределом функции f (x) в точке  x₀ в случае, если для всякого вперёд взятого неотрицательного числа ε будет найдено соответствующее ему неотрицательно число δ = δ(ε) такое, что для каждого аргумента x, удовлетворяющего условию 0 < | x – x0 | < δ, будет выполнено неравенство | f (x) A | < ε.

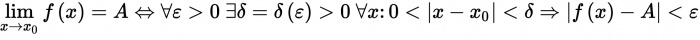
Найти предел функции.

Найти предел функции - будет очень просто, если вы понимаете суть предела и основные правила нахождения его. То, что предел функции f (x) при x стремящемся к a равен A, записывается таким образом:

Причем значение, к которому стремится переменная x, может быть не только числом, но и бесконечностью (∞), иногда +∞ или -∞, либо предела может вообще не быть.

Чтоб понять, как находить пределы функции, лучше всего посмотреть примеры решения.

Пример 1:

Необходимо найти пределы функции f (x) = 1/x при:

 x → 2, x → 0, x → ∞.

Найдем решение первого предела. Для этого можно просто подставить вместо x число, к которому оно стремится, т.е. 2, получим:

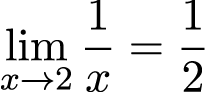
Найдем второй предел функции. Здесь подставлять в чистом виде 0 вместо x нельзя, т.к. делить на 0 нельзя. Но мы можем брать значения, приближенные к нулю, к примеру, 0,01; 0,001; 0,0001; 0,00001 и так далее, причем значение функции f (x) будет увеличиваться: 100; 1000; 10000; 100000 и так далее. Т.о., можно понять, что при x → 0 значение функции, которая стоит под знаком предела, будет неограниченно возрастать, т.е. стремиться к бесконечности. А значит:

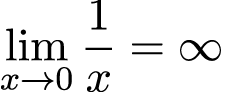
Касаемо третьего предела. Такая же ситуация, как и в прошлом случае, невозможно подставить ∞ в чистом виде. Нужно рассмотреть случай неограниченного возрастания x. Поочередно подставляем 1000; 10000; 100000 и так далее, имеем, что значение функции f (x) = 1/x будет убывать: 0,001; 0,0001; 0,00001; и так далее, стремясь к нулю. Поэтому:

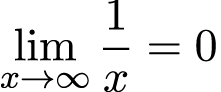
Ответ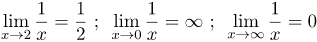

Пример 2:

Необходимо вычислить предел функции 

Приступая к решению второго примера, видим неопределенность . Отсюда находим старшую степень числителя и знаменателя – это x³, выносим в числителе и знаменателе его за скобки и далее сокращаем на него:

Ответ

Пример 3:

Необходимо рассчитать предел   

Первым шагом в нахождении этого предела, подставим значение 1 вместо x, в результате чего имеем неопределенность . Для её решения разложим числитель на множители, сделаем это методом нахождения корней квадратного уравнения x² + 2x  - 3:

D = 2² – 4*1*(-3) = 4 +12 = 16 → √D = √16 = 4

x_1,2  = (-2 ± 4) / 2 → x₁ = -3; x₂ = 1.

Таким образом, числитель будет таким:

Далее сокращаем числитель и знаменатель на (x – 1):

Ответ

Решение пределов функции.

Решение пределов функции - это определение его конкретного значения или определенной области, куда попадает функция, которая ограничена пределом.

Чтобы решить пределы, следуйте правилам:

1. Пробуем подставить в функцию число, результат решения и будет ответом.
2. Если х стремится не к числу, например в пределах вида  или , то такие пределы решаются сразу, так как число, деленное на бесконечность, всегда дает 0, а деленное на нуль это и есть ∞. Если вам сложно понять саму суть бесконечности и нуля в пределах, то подставляйте вместо ∞ - бесконечно большое число – к примеру 1000 000, либо вместо нуля - бесконечно малое - например 0,000001 и после этого можете предположить к чему стремится ответ.
3. Существует группа пределов, в которых и в числитель, и в знаменатель при подстановке получаем либо нуль либо ∞. Это т.н. пределы с неопределенностью, часть из которых замечательные. 

Разобравшись в сути и основных правилах решения предела, вы получите базовое понятие о том, как их решать.