Основное уравнение молекулярно-кинетической теории устанавливает связь между давлением идеального газа и средней кинетической энергией его молекул.
Вывод основного уравнения молекулярно-кинетической теории основывается на допущениях модели идеального газа и утверждении: давление газа является результатом ударов молекул о стенку сосуда.
Определим давление газа на стенку площадью S сосуда ABCD.

Каждая молекула массой m0, отскакивая от стенки после упругого соударения со стенкой, передает ей импульс 2m0vx, где vx — проекция скорости молекулы 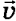 на ось Ох, перпендикулярную стенке. Всего за одну секунду суммарный импульс, получаемый стенкой от всех молекул, равен 2m0vxZ, где Z — число таких столкновений (за 1 с) всех молекул. Очевидно, что
на ось Ох, перпендикулярную стенке. Всего за одну секунду суммарный импульс, получаемый стенкой от всех молекул, равен 2m0vxZ, где Z — число таких столкновений (за 1 с) всех молекул. Очевидно, что 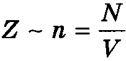 , где n — концентрация молекул в единице объема; N — число всех молекул. Число Z пропорционально также скорости молекул vx и площади стенки S: Z~ nvxS. Поскольку все направления при хаотичном движении молекул газа равновероятны, то из всех молекул, имеющих составляющую скорости vx, только половина движется в сторону стенки CD, вторая половина — в сторону АВ (т.е. в обратную). Поэтому
, где n — концентрация молекул в единице объема; N — число всех молекул. Число Z пропорционально также скорости молекул vx и площади стенки S: Z~ nvxS. Поскольку все направления при хаотичном движении молекул газа равновероятны, то из всех молекул, имеющих составляющую скорости vx, только половина движется в сторону стенки CD, вторая половина — в сторону АВ (т.е. в обратную). Поэтому 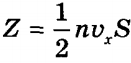 , а полный импульс, переданный стенке за 1 с, равен 2m0vxZ = m0nvx2S. Поскольку изменение импульса точки (тела) за единицу времени равно действующей на него силе
, а полный импульс, переданный стенке за 1 с, равен 2m0vxZ = m0nvx2S. Поскольку изменение импульса точки (тела) за единицу времени равно действующей на него силе 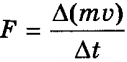 . В действительности, поскольку речь идет о большом количестве молекул, движущихся с разными скоростями, силу следует усреднить:
. В действительности, поскольку речь идет о большом количестве молекул, движущихся с разными скоростями, силу следует усреднить:  .
.
Сила эта зависит, таким образом, от среднего квадрата скорости  . Поскольку вследствие хаотичности движения все направления равноправны, то:
. Поскольку вследствие хаотичности движения все направления равноправны, то:

С другой стороны, известно, что квадрат модуля любого вектора равен сумме квадратов его проекций на оси координат, поэтому:

Усредняя это выражение по всем молекулам и учитывая  , получим:
, получим:

Отсюда:
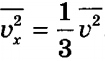
С учетом последней формулы 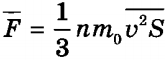 .
.
Следовательно, давление на стенку сосуда равно:

Это основное уравнение молекулярно-кинетической теории. Это уравнение — первое количественное соотношение, полученное в молекулярно-кинетической теории. Уравнение  позволяет получить связь между давлением и средней кинетической энергией молекул
позволяет получить связь между давлением и средней кинетической энергией молекул  .
.
 .
.
Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.
Важно подчеркнуть, что здесь речь идет о средней кинетической энергии молекул газа. Это означает, что давление газа — величина, органически связанная с тем, что газ состоит из большого числа молекул. Нет смысла говорить о давлении, создаваемом несколькими молекулами. Давление газа – понятие, имеющее статистический характер (так называют понятия, имеющие смысл только для систем с очень большим числом частиц).
 Электромагнитные колебания
Электромагнитные колебания


