Кинематика. Сложение скоростей.

С помощью закона сложения скоростей определяется скорость материальной точки относительно неподвижной системы отсчета. Она равна сумме скорости точки относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы:

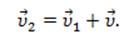
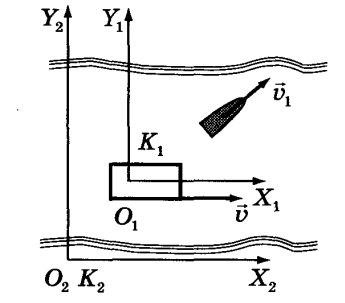
Рассмотрим движение одного и того же тела относительно двух тел отсчета, движущихся друг относительно друга. Для простоты допустим, что одно из тел отсчета неподвижно, а второе движется относительно первого прямолинейно и равномерно.

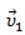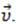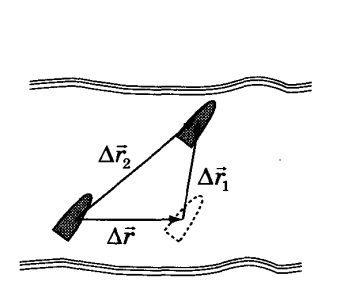
Лодка плывет со скоростью  по реке (система отсчета К₁). За неподвижное тело примем берег (система отсчета К₂), а за подвижное – воду и обозначим скорость ее движения относительно берега через  Векторы перемещений лодки относительно воды , реки относительно берега  и суммарный вектор перемещения лодки относительно берега 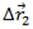 изображены на рисунке. Математически это можно выразить уравнением:

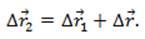
Поделив обе части уравнения на Δt, мы получим:

что равносильно первому уравнению.

Вместо векторов воспользовавшись их проекциями на оси координат, получим:

υ_2x = υ_1x + υ_x,

υ_2y = υ_1y + υ_y.

Проекции скоростей складываем алгебраически.