Дифференциальное уравнение 2-го порядка записывают как:
.
В ДУ 2-го порядка всегда входит 2-я производная 
и не входят производные более высоких порядков:
Обратите внимание, что некоторые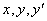 
(или все сразу) могут отсутствовать в уравнении, но обязательно должен быть .
Самое примитивное дифференциальное уравнение второго порядка имеет такой вид:
.
Для этих уравнений есть теорема существования и единственности решения:
Теорема. Если в уравнении 
функция 
и ее частные производные по аргументам y и 
непрерывны в некоторой области, которая содержит 
, то есть единственное решение 
уравнения, которое удовлетворяет условиям 
и 
.
Эти условия являются начальными условиями. Геометрический смысл этих условий состоит в том, что через заданную точку плоскости 
с заданным tg угла наклона касательной 
проходит единственная интегральная кривая.
Видно, что если задавать различные значения 
, то при постоянных 
и 
будет получено бесконечное число интегральных кривых с разными углами наклона касательных и проходящих через заданную точку.
Общим решением дифференциального уравнения второго порядка является функция 
, которая зависит от 2-х произвольных постоянных, которая при любых значениях С1 и С2 будет решением ДУ.
Уравнение 
, которое определяет общее решение, является общим интегралом дифференциального уравнения.
Подставив конкретные значения С1 и С2 в общее решение, получим частное решение дифференциального уравнения. График частного решения является интегральной кривой данного дифференциального уравнения.
Дифференциальные уравнения второго порядка делятся на:
- Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- Линейные однородные дифференциальные уравнения (ЛОДУ) и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка.